DIY Higgs: anything's possible with ROOT!

Hey physicists! Lack of an observed Higgs boson getting you down? Well fret no longer: you can make your own, thanks to the miracle of ROOT! Look, here's one I made earlier:

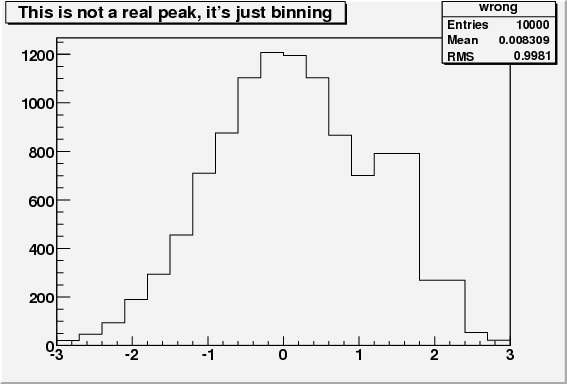
Okay, so everything's wrong: it's not a very good impression of a Higgs, I know (and let's not even mention the dismal message that this sends about physicist aesthetics and the attention paid to typesetting by the ROOT authors) But this is a worrying effect, given that this is the CINT macro that produced it:

{
    double edges[19] = {-3.0, -2.7, -2.4, -2.1, -1.8, -1.5, -1.2, -0.9, -0.6, -0.3, 0.0, 0.3, 0.6, 0.9, 1.2, 1.8, 2.4, 2.7, 3.0};
    // Double-size bins                          ^    ^
    TH1F h("wrong", "This is not a real peak, it's just binning", 18, edges);
    h.FillRandom("gaus", 10000);
    h.SetMinimum(0.0);
    h.Draw();
}

Yes, that plot is a random Gaussian distribution, according to ROOT. The big peak on the RHS is created by the two bins of width 0.6 (as opposed to 0.3 everywhere else). I hope it's obvious that this is wrong! If it were a bar graph where the width of bins has no meaning, then it would be correct, but the idea of a histogram is that bin heights are set by the sum of weights in the bin divided by the bin width. Or, expressed as they tell you at school, a histogram's area, rather than height, is the thing that reflects the number of "events" in that bin. For differential distributions (i.e. densities), which account for about 99% of all physics distributions, histograms are the only sensible statistical display to use, since they maintain the distribution's shape as an invariant under arbitrary rebinnings: with asymptotically high statistics, a histogram should have heights equal to the mean value of the true distribution between the bin edges, a criterion which bar plots do not satisfy. Or, more loosely speaking, the choice of bin edge position on a distribution shouldn't have any significance!

This is a silly mistake, a schoolboy error. It's like trying to uniformly sample a spherical surface without accounting for the d(cos(theta)) measure factor: the 1D measures here are the bin widths. And it's a dangerous error from a physics perspective, as the plot above shows: in a real physics analysis, it's conceivable that you would bin more tightly around a region of interest, like a potential Higgs peak, in which case ROOT would actually display a dip! It's amazing that no one seems to have noticed this in 15+ years of ROOT being used by the HEP community. I don't use ROOT enough to know if this is a known issue --- students and postdocs that I've mentioned this to have been surprised. Maybe it reflects the tendency of the community to make private work-arounds rather than report bugs upstream --- not that my experiences of trying to report bugs on ROOT have been very encouraging --- or just that with the lack of LHC data no- one has made any non-uniformly binned histograms yet!

Given that my gripes against ROOT are well-publicised, it's with some trepidation (albeit also a fair chunk of smugness) that I'm writing this, but this issue needs to be publicised and fixed. The fix, fortunately, is just for the rendering system to include the width factor when calculating bin heights: the API's GetBinData(index) function name doesn't imply anything wrong about heights, it's just being used inappropriately. Fixing it should definitely be done, and wouldn't be hard, but it's difficult to know how much existing code relies on this behaviour.